
트리문제이기도 하지만 분할정복으로 문제를 해결하므로 분할정복 카테고리에 삽입한
정답률 37퍼센트의 트리의 순회 문제이다,
문제는 1부터n까지 번호의 트리가 있을 때
인오더와 포스트오더가 주어지고
프리오더로 출력하면 되는 문제이다.
트리의 탐색 방법인 프리오더, 인오더, 포스트오더에 대해 까먹었었는데
이번엔 정말 외워야 겠다.
preOrder(프리오더)
- Root, Left, Right순으로 방문한다.
inOrder(인오더)
- Left, Root, Rigth순으로 방문한다.
postOrder(포스트오더)
- Left, Rigth, Root순으로 방문한다.
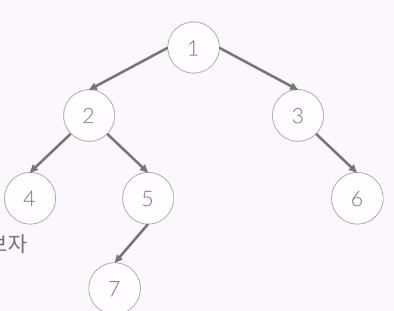
이런 자료구조가 있을 때
프리오더는 1 2 4 5 7 3 6
인오더는 4 2 7 5 1 3 6
포스트오더는 4 7 5 2 6 3 1
인 것이다.
문제로 돌아가서
포스트 오더를 통해 알 수 있는 것이 있다.
바로 루트의 번호이다.
포스트 오더는 Left -> Rigth -> Root 순으로 탐색하기 때문에
맨 마지막에는 가장 위에 있는 Root가 오는 것이다.
인오더는 Left -> Root -> Rigth 순으로 탐색하기 때문에
포스트오더를 통해 알아낸 루트를 주어진 인오더에서 인덱스를 찾으면
왼쪽과 오른쪽을 구분 할 수 있다.
이렇게 구분해서 왼쪽 자식의 수를 알아낸 다음
인오더의 왼쪽, 포스트오더의 왼쪽 메소드를 호출,
인오더의 오른쪽, 포스트오더의 오른쪽 메소드를 호출하면서
알아낸 루트를 계속 출력하면
루트 -> 왼쪽 -> 오른쪽으로 탐색하는 프리오더와 똑같이 출력할 수 있다.
인오더
4 2 7 5 /1/ 3 6
포스트오더를 통해 알아낸 1의 인덱스 4를 기준으로
0~3 -> 4 2 7 5 는 왼쪽 자식
5~6 -> 3 6 은 오른 쪽 자식 인것이다.
이를 통해 왼쪽 자식의 수와 오른쪽 자식의 수를 알 수 있다.
포스트오더에서는
4 7 5 2 6 3 1
1인 루트를 제외하고
왼쪽 자식의 수인 크기 4만큼 4 7 5 2 가 왼쪽 자식이고
6 3이 오른쪽 자식 인 것이다.
이렇게 알아낸
인오더의 왼쪽자식, 포스트오더의 왼쪽 자식의 인덱스,
인오더의 오른쪽자식, 포스트오더의 오른쪽 자식의 인덱스,
을 매개변수로 해서 메소드를 다시 호출하면 된다.
인오더의 루트 인덱스를 알아낼 땐
인오더를 하나하나 탐색하면 메소드 호출 시마다 O(n)만큼의 시간이 소요되므로
position이라는 배열을 따로 만들고
인오더의 위치를 삽입하여
메소드의 호출 시간을 O(1)으로 만든다.
설명을 잘 못한 것 같다. 코드를 보면서 이해하는게 더 빠를 것 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public class Q2263 {
static int [] inOrder = new int[100000];
static int [] postOrder = new int[100000];
static int [] position = new int[100001];
static void solve(int is, int ie, int ps, int pe) {
if(is>ie || ps>pe) return ;
int root = postOrder[pe];
System.out.print(root+" ");
int inRoot = position[root]; //인오더의 루트 인덱스
int left = inRoot-is; //포스트오더의 왼쪽 자식의 수
solve(is, inRoot-1, ps, ps+left-1);
solve(inRoot+1, ie, ps+left, pe-1);
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
for(int i=0; i<n; i++)
inOrder[i] = scan.nextInt();
for(int i=0; i<n; i++)
postOrder[i] = scan.nextInt();
for(int i=0; i<n; i++)
position[inOrder[i]] = i;
solve(0, n-1, 0, n-1);
}
}
|
'Algorithm' 카테고리의 다른 글
| 백준 2631 & 7570 줄 세우기 Java (0) | 2019.05.22 |
|---|---|
| 백준 1074 Z Java (0) | 2019.05.20 |
| 백준 11729 하노이 탑 이동 순서 Java (0) | 2019.05.17 |
| 백준 2873 롤러코스터 Java (0) | 2019.05.15 |
| 백준 1107 리모컨 Java (0) | 2019.05.14 |