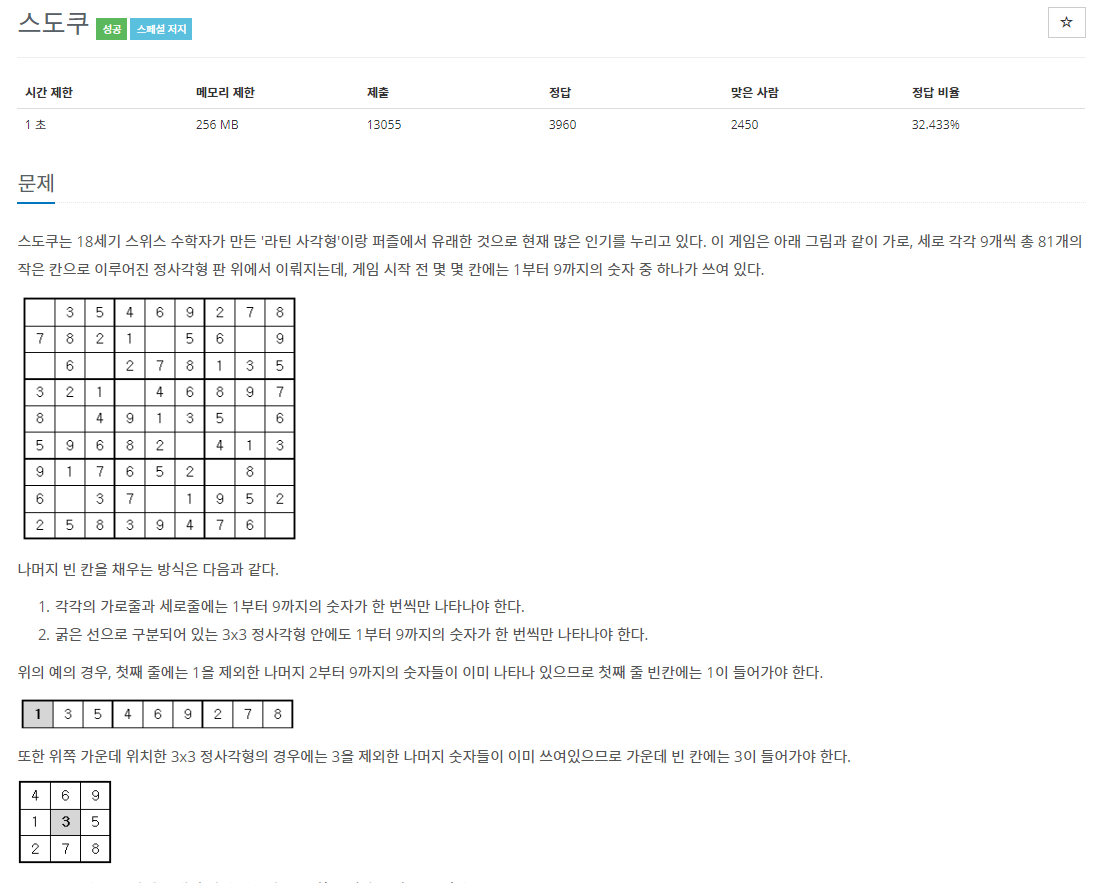

N-Queen과 함께 백트래킹하면 떠오르는 문제라는 스도쿠 문제이다.
스도쿠는 다들 아는 것 처럼 하나의 행에서 1~9, 하나의 열에서 1~9, 3*3 사이즈의 행렬에서 1~9가 있어야 한다.
처음에는 유튜브의 영상을 참고하며 무난하게 백트래킹의 정석대로 문제를 풀었었다.
스도쿠의 규칙을 어기는지 검사하는 check 메소드를 하나 만들어
0을 만났을 때 1부터 9까지 숫자를 넣어보며 check가 true일 때 다음 단계를 진행했다.
0을 만날때 마다 1~9까지 가능한 수를 삽입하고 다시 검사하기 때문에 시간 초과가 나왔다.
check 메소드를 보면
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public static boolean check(int[][]a) {
boolean[]b = new boolean[9];
for(int i=0; i<3; i++) {
for(int j=0; j<9; j++) {
Arrays.fill(b, false);
for(int k=0; k<9; k++) {
int v = 0;
if(i==0) { //행 검사
v = a[j][k];
}else if(i==1) { //열 검사
v = a[k][j];
}else {
v = a[j/3*3+k/3][j%3*3+k%3];
}
if(v==0) continue;
if(b[v-1]) return false;
b[v-1] = true;
}
}
}
return true;
}
|
3중 for문으로
i가 0일땐 행을 검사하고 i가 1일 땐 열을 검사하고 i가 2일 땐 3*3의 작은 사각형을 검사했다.
이 문제에서 가장 까다로운 부분이 3*3의 작은 사각형 부분인 것 같다.
boolean형 배열으로 1~9까지의 인덱스를 모두 false로 놓고
수가 나올때마다 true로 바꿔준다.
만약 이미 true로 바꿔진 수가 또 나온다면
같은 수가 두 번있는 것이므로 false를 리턴한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
public static void go(int[][]a, int cnt) {
if(cnt == 81) {
for(int i=0; i<9; i++) {
for(int j=0; j<9; j++) {
System.out.print(a[i][j]+" ");
}
System.out.println();
}
System.exit(0);
}
int row = cnt/9;
int col = cnt%9;
int v = a[row][col];
if(v != 0) {
go(a, cnt+1);
}else {
for(int i=1; i<=9; i++) {
a[row][col] = i;
if(check(a)) {
go(a, cnt+1);
}
}
a[row][col] = 0;
}
}
|
그리고 스도쿠의 마지막인 81번째까지 진행됐다면 스도쿠를 출력하고 프로그램을 종료한다.
몇 번째 인지 하나의 정수로 검사하기 때문에
행과 열을 구할 땐 /9와 %9로 구하였다.
하지만 이 코드는 시간 초과가 나왔다.
의문인 점은 가장 오래 걸리는 경우가 전부 0인 경우일 거라 생각하고
전부 0인 경우가 빠른시간안에 통과되는 것을 보고 정답이라고 생각했는데
시간 초과가 나왔다. 더 오래 걸리는 경우가 어떤 경우이고 왜 그런지 모르겠다.
질문을 등록해놨으니 일단 기다려야 겠다.
그리고 더 빠르게 할 수 있는 경우를 백준 님의 풀이로 공부했다.
백준 님은 풀이는 N-Queen문제와 거의 비슷한 방식이었다.
위와 비슷하게 81번째 라면 스도쿠를 출력하고
행과 열을 구한다.
2차원 배열로 행 체크 배열, 열체크 배열, 작은 사각형 체크 배열을 만든다.
i번째 행일 때 1이 있다면 [i][1]에 true를 넣고
j번째 열일 때 1이 있다면 [j][1]에 true를 넣고
가장 까다로운 부분인 작은 사각형 부분은

0번째 작은 사각형, 1번째 작은 사각형... 8번째 작은 사각형으로 분류하여
i번째 작은 사각형에 1이 있다면 [i][1]에 true를 넣었다.
몇 번째 작은 사각형인지 구하는 방법은
(i / 3) * 3 + j / 3이다.
이렇게 수를 입력 받음과 동시에
각각의 check배열을 true로 초기화해주고
1부터 9까지 수를 대입해보며 각각의 check배열에 false라면
각 check배열을 true로 바꿔주고
0인 자리를 해당 수로 초기화한다.
그 후 +1 해주고 재귀 호출을 한다.
백트래킹을 해야 하기 때문에
각 check배열을 false로
바꾼 수를 다시 0으로 바꿔준다.
여기서 중요한 점은 81번째 됐을 때
출력 후 프로그램을 종료시키는 System.exit(0)이다.
출력 후 프로그램을 종료시키지 않는다면 남아있는 재귀 호출을 전부 다 실행하면서
시간 초과가 나오게 된다.
문제에서 스도쿠가 완성되는 경우가 여러 가지일 때는 하나만 출력하면 된다고 했으므로
첫 번째 완성했을 때 프로그램을 종료시켜버림으로써 시간 초과를 피할 수 있다.
지저분한 설명보다 코드를 통해 이해하는 것이 빠를 것 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
public class Q2580_ver2 {
static boolean [][] rowCheck = new boolean[9][10];
static boolean [][] colCheck = new boolean[9][10];
static boolean [][] squareCheck = new boolean[9][10];
static int square(int x, int y) { //몇번째 작은 사각형인지 계산
return (x/3)*3+y/3;
}
public static void go(int[][]a, int cnt) {
if(cnt == 81) {
for(int i=0; i<9; i++) {
for(int j=0; j<9; j++) {
System.out.print(a[i][j]+" ");
}
System.out.println();
}
System.exit(0); //더 이상 재귀가 돌지 않도록 프로그램 종료, 없으면 시간초과
}
int x = cnt/9; //행 구하기
int y = cnt%9; //열 구하기
if(a[x][y] != 0) {
go(a, cnt+1);
}else {
for(int k=1; k<=9; k++) {
if(!rowCheck[x][k] && !colCheck[y][k] && !squareCheck[square(x,y)][k]) { //3가지 경우 모두 k가 없을 경우
rowCheck[x][k] = true; //다시 방문하지 않기위한
colCheck[y][k] = true;
squareCheck[square(x,y)][k] = true;
a[x][y] = k; //0을 k로 바꿈
go(a, cnt+1); //다음 단계
//백트래킹을 위한
a[x][y] = 0;
rowCheck[x][k] = false;
colCheck[y][k] = false;
squareCheck[square(x,y)][k] = false;
}
}
}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int [][] a = new int[9][9];
for(int i=0; i<9; i++) {
for(int j=0; j<9; j++) {
a[i][j] = scan.nextInt();
if(a[i][j] != 0) {
rowCheck[i][a[i][j]] = true;
colCheck[j][a[i][j]] = true;
squareCheck[square(i, j)][a[i][j]] = true;
}
}
}
go(a, 0);
}
}
|
작은 사각형을 처리하는 부분을 생각해내는 것이 어려운 것 같다.
'Algorithm' 카테고리의 다른 글
| 백준 2210 숫자판 점프 Java (0) | 2019.06.24 |
|---|---|
| 백준 14502 연구소 Java (1) | 2019.06.18 |
| 백준 2437 저울 Java (0) | 2019.06.14 |
| 백준 1138 한 줄로 서기 Java (4) | 2019.06.13 |
| 백준 9663 N-Queen Java (0) | 2019.06.13 |