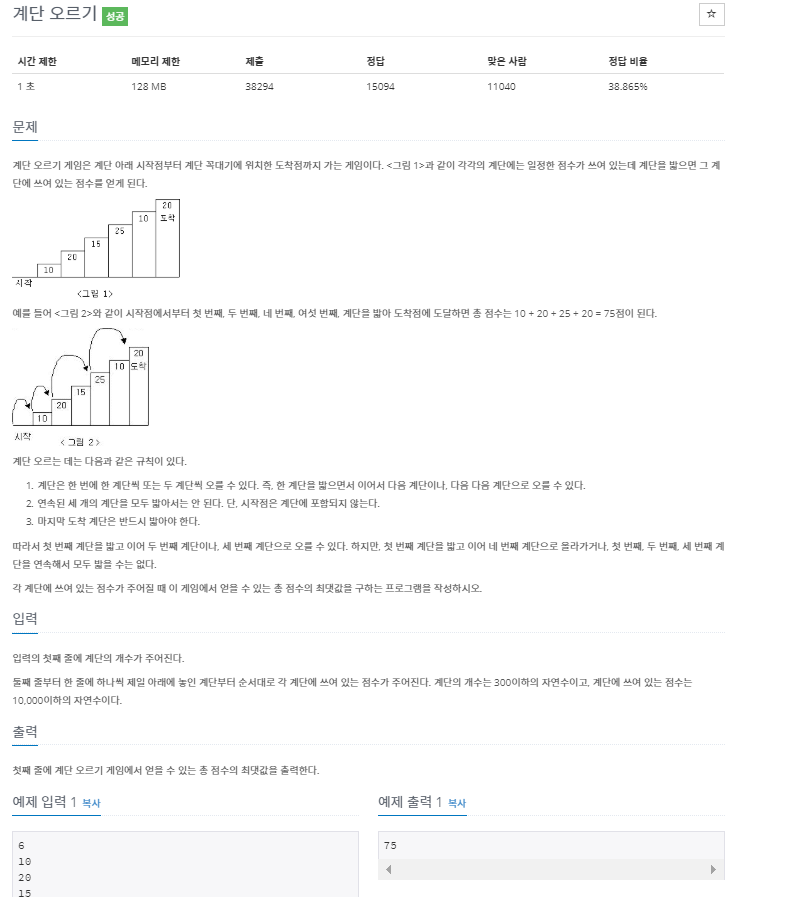
정답률 38퍼센트의 dp문제이다. 백준에서 많이 풀려진 dp문제 중 하나이다.
다음 다음 계단으로 한번에 오르거나 다음 계단으로 오르거나 둘 중에 하나이다.
그리고 계단을 세 번 연속으로 오를 수 없다는 조건이 있다.
n-1에 올 수 있는 경우에 수는 두 가지 있다.
두 번 연속으로 오른 경우와
첫 번째 계단인 경우
첫 번째 계단인 경우는 바로 전 계단을 오르지 않았을 경우다. 그렇기 때문에
전 전 계단 값 + 현재 값이다. dp[n] = dp[n-2]+값[n]
두 번째 계단인 경우는 현재 계단 값 + 전 계단 값 + 전전전 계단값을 더해야 한다.
여기서 현재 계단 값과 전 계단 값을 dp배열에서 더하지 않고 입력 받은 값이 들어있는 배열에서
더해 줌으로 써 세번 연속으로 계단을 오르지 않는다는 규칙을 지킬 수 있다.
점화식은 dp[n] = dp[n-3]+ 값[n-1]+값[n]이다.
그리고 이 두가지 경우 중 더 큰 값이 dp배열에 들어가는 것이다.
dp[n]= Math.max(dp[n-1]+값[n], dp[n-3]+값[n-1]+값[n]);
또한 2차원 배열로 첫 번째 계단인 경우와 두 번 연 속오른 경우를 나눠서
풀 수 도있다. 코드에 주석부분에 해당한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public static void main(String [] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int [] a = new int[n+1];
int [] dp = new int[n+1];
for(int i=1; i<=n; i++)
a[i] = scan.nextInt();
dp[1] = a[1];
dp[2] = a[1]+a[2];
for(int i=3; i<=n; i++)
System.out.println(dp[n]);
// 2차원으로 풀이
// Scanner scan = new Scanner(System.in);
// int n = scan.nextInt();
// int [] a = new int[n+1];
// int [][]dp = new int[n+1][2];
//
// for(int i=1; i<=n; i++)
// a[i] = scan.nextInt();
//
// dp[1][0] = a[1];
//
// for(int i=2; i<=n; i++) {
// dp[i][0] = Math.max(dp[i-2][0],dp[i-2][1])+a[i]; //첫번째 계단인 경우
// dp[i][1] = dp[i-1][0]+a[i]; //두번 째 계단인 경우
// }
}
|
'Algorithm' 카테고리의 다른 글
| 백준 2133 타일채우기 Java (0) | 2019.04.15 |
|---|---|
| 백준 1699 제곱수의 합 Java (1) | 2019.04.15 |
| 백준 1912 연속합 Java (0) | 2019.04.12 |
| 백준 11053 가장 긴 증가하는 부분 수열 Java (0) | 2019.04.12 |
| 백준 2156 포도주 시식 Java (0) | 2019.04.10 |