
타일 채우기 문제이다.
왜 정답률이 35퍼센트인지 모르겠다. 10~19퍼센트는 되야 할 것 같은데..
2xn타일링 문제랑 비슷한 문제이다. 그래서 비슷하게 접근했다가 바로 틀려버렸다.
마지막 자리에 올 수 있는 타일의 형태는

이렇게 3가지의 형태라고 생각했고. 저 형태들 앞은 n-2이기 때문에
dp[n] = dp[n-2]*3; 이라고 간단하게 생각했다. 2xn타일링 문제에선 그랬으니까.
하지만

이렇게도 형태가 나올 수 있고.
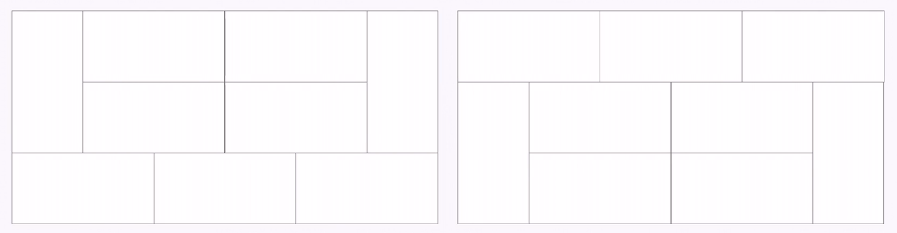
이렇게도 나올 수 있다.
더 나아가 위에 그림에 가로 타일을 추가하고 안에 가로타일을 추가해주는 방법도 있다.
결론적으로 이 문제의 마지막 자리에 올 수 있는 형태는
dp[n-2]*3 + dp[n-4]*2 + dp[n-6]*2 ... dp[0]*2 까지 다 올 수 있는 것이 였다.
점화식 또한 dp[n] = dp[n-2]*3 + dp[n-4]*2 + dp[n-6]*2 ... dp[0]*2 ; 이다.
이 것을 어떻게 저 문제만 보고 떠올릴 수 있는지 참 신기하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int [] dp = new int[n+1];
dp[0] = 1;
for(int i=2; i<=n; i++) {
dp[i] = 3*dp[i-2];
for(int j=i-4; j>=0; j-=2)
dp[i]+=2*dp[j];
}
System.out.println(dp[n]);
}
|
'Algorithm' 카테고리의 다른 글
| 백준 11005 진법 변환 2 Java (0) | 2019.04.15 |
|---|---|
| 백준 2609 최대공약수와 최소공배수 Java (0) | 2019.04.15 |
| 백준 1699 제곱수의 합 Java (1) | 2019.04.15 |
| 백준 2579 계단오르기 Java (0) | 2019.04.14 |
| 백준 1912 연속합 Java (0) | 2019.04.12 |