
정답률 15퍼센트의 가장 가까운 두 점 문제이다.
정답률에서도 알 수 있듯이 굉장히 어려운 문제인 것 같다..
n의 최댓값이 100000, 십만으로 O(n^2)으로 비교하는 간단한 알고리즘으로는 절대 풀 수 없다.
당연히 나도 풀 수 없었고, 백준님의 강의를 토대로
'분할 정복'으로 푼 가장 가까운 두 점 문제를 정리하려고 한다.
푸는 방법은 이렇다.
x좌표 순으로 정렬을 한다.

그리고 중간 인덱스를 기준으로
왼쪽에서 가장 가까운 두점 사이의 거리를 찾고
오른쪽에서 가장 가까운 두점 사이의 거리를 찾는다.
왼쪽에서 구한 값과 오른쪽에서 구한 값 중 더 작은 값을 저장한다.
중간값을 기준으로 왼쪽, 오른쪽에서 가장 가까운 두점 사이의 거리는 찾았다.
남은 것은 중간값을 지나는 왼쪽 점과 오른쪽 점 사이의 거리를 비교해보면 된다.
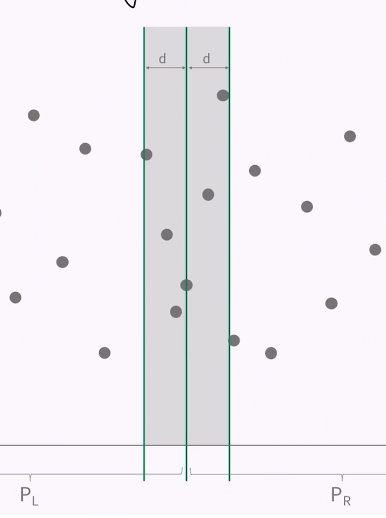
왼쪽 점과 오른쪽 사이의 점 거리를 비교할 때
왼쪽 점 전부와 오른쪽 점 전부를 비교해 볼 필요는 없다.
가장 가까운 점을 찾는 것이기 때문에
앞에서 구한 왼쪽, 오른쪽에서 가장 가까운 두점 사이의 거리 보다 멀리 떨어진 점들은 볼 필요가 없다.

이렇게 중간 인덱스를 기준으로 앞에서 구한값인 d만큼의 거리 안쪽에 점만 살펴보면 되는데
이 점들은 중간인덱스의 점을 기준으로 최대 6개, 9개이다.
x좌표 순으로 정렬을 했기 때문에
x좌표와 중간값의 거리의 제곱이 구한 값인 d보다 작은 점들만 따로 ArrayList에 넣어준다.
x좌표와 중갑값의 거리의 제곱이 d보다 큰 경우엔 정답이 될 수 없다.
그리고 그 ArrayList를 다시 y좌표 순으로 정렬해서
점들의 y좌표들 간의 거리의 제곱이 d보다 작은 값들만 거리를 구해서
서로 비교하며 최솟값을 찾으면 된다.
사실 코드를 보면서 이해하는게 훨씬 쉽다.
코드가 긴편이지만 두 세번만 읽어보면 뭐하는 코드인지는 알 수 있다..
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.StringTokenizer;
public class Q2261 {
static int dist(Point p1, Point p2) { //두 좌표사이의 거리를 구하는 메소드
return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
static int bruteForce(List<Point> a, int x, int y) { //완전 탐색으로 가장 가까운 거리 찾기
int ans = -1;
for(int i=x; i<=y-1; i++) {
for(int j=i+1; j<=y; j++) {
int k = dist(a.get(i), a.get(j));
if(ans == -1 || ans > k)
ans = k;
}
}
return ans;
}
static int closest(List<Point> a, int x, int y) {
int n = y-x+1;
if(n <= 3) { //n이 3이하면 완전탐색으로 x부터 y까지 가장 가까운 두 점 사이의 거리를 찾는다.
return bruteForce(a, x, y);
}
int mid = (x+y)/2;
int left = closest(a, x, mid);
int right = closest(a, mid+1, y);
List<Point> b = new ArrayList<>(); //왼쪽과 오른쪽 사이의 점들을 저장할 List
for(int i=x; i<=y; i++) {
int d = a.get(i).x - a.get(mid).x;
if(d*d < ans) {
b.add(a.get(i));
}
}
int m = b.size();
for(int i=0; i<m-1; i++) {
for(int j=i+1; j<m; j++) {
int k = b.get(j).y - b.get(i).y;
if(k*k < ans) {
int d = dist(b.get(i), b.get(j));
if(d < ans) {
ans = d;
}
}
else { //y좌표 순으로 정렬했기 때문에 앞의 가장 가까운 점이 ans보다 크면 더 볼필요가 없다.
break;
}
}
}
return ans;
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(reader.readLine());
List<Point> a = new ArrayList<>();
for(int i=0; i<n; i++) {
StringTokenizer st = new StringTokenizer(reader.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
a.add(new Point(x, y));
}
System.out.println(closest(a, 0, n-1));
}
}
class PointComparator implements Comparator<Point>{ //y좌표 순으로 정렬하기 위한 Comparator
@Override
public int compare(Point o1, Point o2) {
return o1.y-o2.y;
}
}
class Point implements Comparable<Point>{
int x;
int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point o) {
int r = this.x - o.x;
if(r == 0)
r = this.y - o.y;
return r;
}
}
|
사실 완벽하게 100% 풀이법을 이해하지는 못했다.
정말 어렵다.
똑같은 문제인 5620번 가장 가까운 두 점 사이의 거리를 풀어보려고 했으나
https://www.acmicpc.net/problem/5620
5620번: 가장 가까운 두 점의 거리
문제 평면상에 n개의 점 (P1, .... , Pn) 이 놓여져있다고 했을 때, 거리가 최소인 두 개의 점을 구하고 그 거리를 알고 싶다. 입력 입력은 첫 번째 줄에 정수로 된 점의 개수 n이 주어진다. 두 번째 줄부터 n+1번째 줄까지 2개의 정수 x,y가 공백을 사이에 두고 주어진다. i+1번째 줄은 Pi 의 x,y 좌표를 의미하고 n개의 점에 대해서 주어지게 된다. 점의 개수는 2 ≦ n ≦ 500000 , 좌표의 범위는 -10000 ≦ x,y
www.acmicpc.net
n의 최대값이 위의 문제(2261)보다 5배나 더크다. 결과는 역시 시간초과였다.
분할정복만으로 푸는 것보다 라인스윕으로 푸는 것이 더 간단할 수도 있으므로
라인스윕 알고리즘을 공부해서 5620번 문제를 풀어봐야 겠다.
'Algorithm' 카테고리의 다른 글
| 백준 2110 공유기 설치 Java (0) | 2019.05.24 |
|---|---|
| 백준 1654 랜선 자르기 Java (1) | 2019.05.23 |
| 백준 7571 점 모으기 Java (0) | 2019.05.22 |
| 백준 1517 버블 소트 Java (0) | 2019.05.22 |
| 백준 2631 & 7570 줄 세우기 Java (0) | 2019.05.22 |