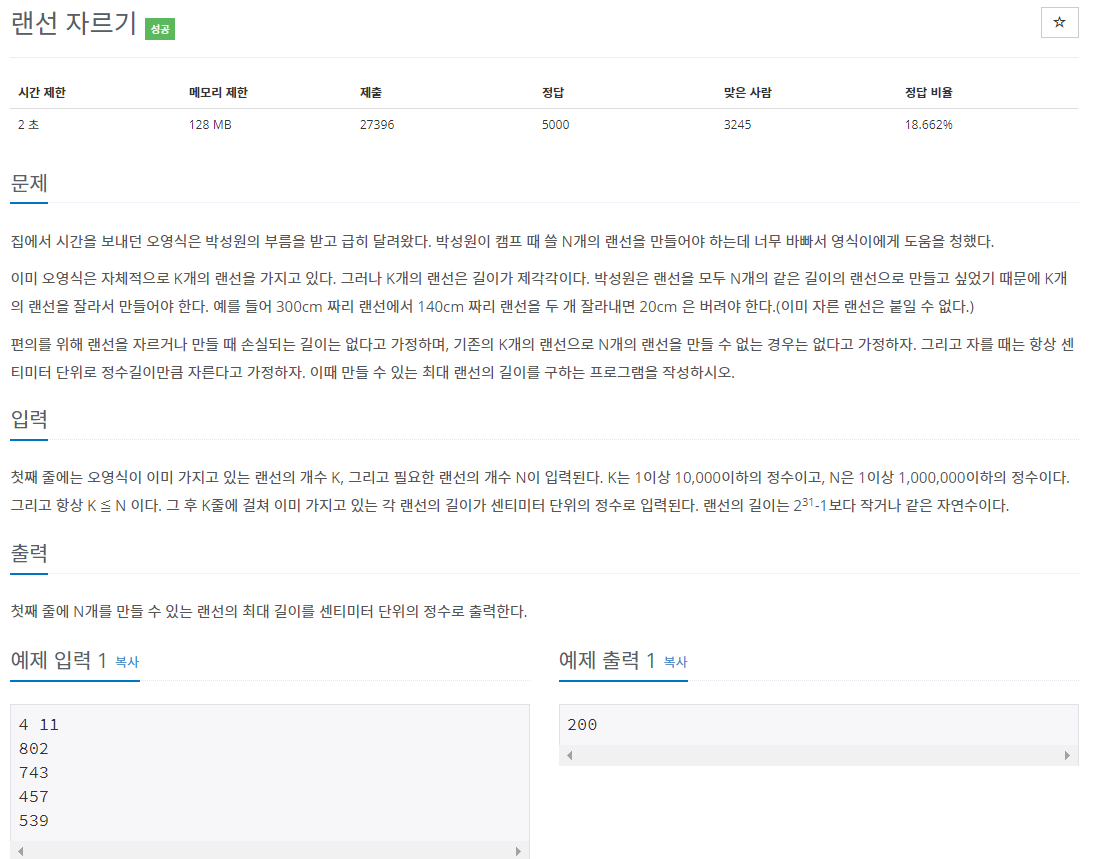
이분 탐색 문제인 랜선 자르기 문제이다.
이미 가지고 있는 랜선 개수 인 k와 만들어야 하는 랜선 개수 n
그리고 k개 만큼의 랜선 길이가 주어진다.
모두 똑같은 길이로 n개의 개수만큼 랜선을 자르려고 할때
최대 길이를 출력하면 된다.
랜선 길이의 최대값이 2^31 -1 이기 때문에
길이를 1부터 최대 길이까지 다 잘라보고 n이상인 것 중 최대값을 찾는 방식으로 풀면
시간 초과가 나올 것이다
어쨌든 길이를 정하고 잘라보면서 개수를 n과 비교하며 찾아야 하는것은 맞다.
범위를 줄여나가는게 중요한 것 같다.
찾아볼 범위의 시작을 start라고 하고
범위의 끝은 end라고 하겠다.
처음에는 당연히 start = 1 일 것이고,
end는 랜선길이중 최대값 일 것이다.
그리고 일단 start와 end의 중간값으로 비교를 한다.
중간값을 mid라고 하겠다.
mid로 k개의 랜선을 잘랐을 때 개수가 n개 이상이면
최대길이는 적어도 mid값 이상이므로
start = mid+1;
n개 이하이면
최대길이는 적어도 mid값 이하이므로
end = mid-1; 로 해준다.
이렇게 비교를 해주면서
개수가 n개 이상일 때의 최대길이를 계속해서 비교해주고
가장 큰 값을 출력하면 된다.
쉬운 코드이므로 코드를 보면 금방 이해가 될 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
public class Q1654 {
public static boolean check(long[] a, int n, long x) {
int cnt = 0;
for (int i=0; i<a.length; i++) {
cnt += a[i]/x;
}
return cnt >= n; //x로 잘랐을 때 n개 이상인지 리턴
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int k = sc.nextInt();
int n = sc.nextInt();
long[] a = new long[k];
long max = 0;
for (int i=0; i<k; i++) {
a[i] = sc.nextLong();
max = Math.max(max, a[i]);
}
long ans = 0;
long start = 1;
long end = max;
while (start <= end) {
long mid = (start+end)/2;
if (check(a, n, mid)) {
ans = Math.max(ans,mid);
start = mid+1;
} else {
end = mid-1;
}
}
System.out.println(ans);
}
}
|
'Algorithm' 카테고리의 다른 글
| 백준 1939 중량제한 Java (0) | 2019.05.24 |
|---|---|
| 백준 2110 공유기 설치 Java (0) | 2019.05.24 |
| 백준 2261 가장 가까운 두 점 Java (2) | 2019.05.23 |
| 백준 7571 점 모으기 Java (0) | 2019.05.22 |
| 백준 1517 버블 소트 Java (0) | 2019.05.22 |