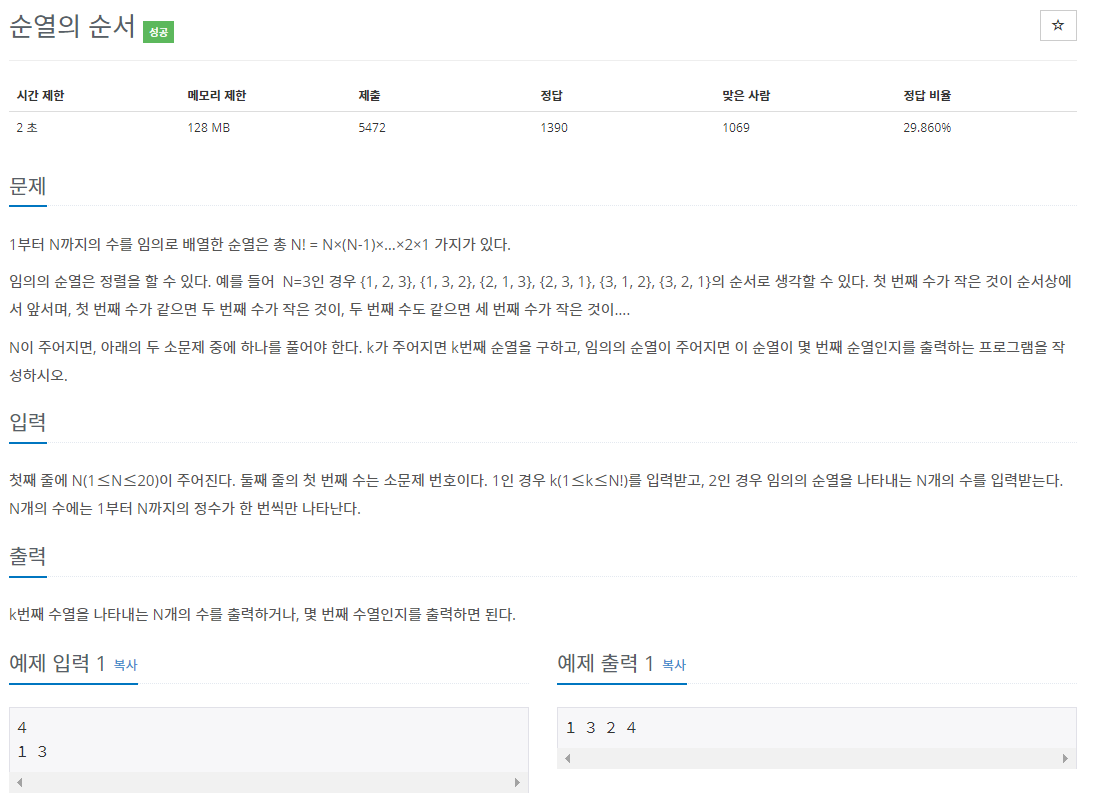
순열의 크기 N이 주어지고
순열이 사전순으로 정렬되어 있을 때
1번과 2번으로 나눈 문제가 주어진다.
1번의 경우에는 순열의 순서 k를 주고
k번째 순열 N개를 출력하면 된다.
2번의 경우에는 순열 N개가 주어지고
순서 k를 출력하면 된다.
N의 최댓값인 20으로
20!까지 순열을 나타낼수 있으므로
순열의 순서를 미리 다 구해놓고 문제를 푸는 방식은 시간초과이다.
2번 문제는
N개의 순열의 개수가 N!개 인 점을 생각해서 문제를 풀면 된다.
N = 7 {5 2 4 7 6 3 1}이 있을 때
첫자리인 5를 보면
5 전에
1로 시작하는 순열 6!개
2로 시작하는 순열 6!개
3으로 시작하는 순열 6!개
4로 시작하는 순열 6!개가 있었을 것이다.
첫자리가 5로 고정일 때
두 번째 자리인 2 전에
5 1로 시작하는 순열 5!개가 있었을 것이다.
5 2 로 고정했을 때
세 번째 자리인 4전에
5 2 1로 시작하는 순열 4!개
5 2 3으로 시작하는 순열 4!개
5 2 4로 고정했을 때
5 2 4 1 로 시작하는 순열 3!개
5 2 4 3 으로 시작하는 순열 3!개
5 2 4 6 으로 시작하는 순열 3!개가 있었을 것이다.
이런 식으로 그 전에 존재할 수 있는 순열의 개수를
더해주는 방식으로 구하면 된다.
이 방식은 순열의 시작이
1번 문제에서는 2번문제에서 구한 방식의 반대로 구해주면 된다.
N = 7이고 k번째 순열을 구한다면
N이 7이기 때문에 첫 번째 자리 수를 구하려면
k에서 6!을 계속 빼준다
만약 k에서 i번째 6!을 뺄 때 6!보다 작아진다면
그 i가 첫 번째 자리 수가 되는것이다.
이런 식으로 쭉쭉 7번째 자리수까지 구하다보면
k는 1이 되어있게 되는 것이다.
이번에도 역시 코드를 보고 이해하는것이 빠를 듯 하다..
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long [] f = new long[21];
boolean [] c = new boolean[21]; //n엔 중복된 수가 없으므로 중복을 없앨 boolean 배열
Arrays.fill(f, 1);
for(int i=1; i<=20; i++) { //팩토리얼 구하기
f[i] = f[i-1]*i;
}
int n = scan.nextInt();
int what = scan.nextInt();
int [] a = new int[n];
if(what == 2) { //몇 번째 순열인지
for(int i=0; i<n; i++)
a[i] = scan.nextInt();
long ans = 1; //순열은 1 번째 부터 시작
for(int i=0; i<n; i++) {
for(int j=1; j<a[i]; j++) {
if(!c[j])
ans += f[n-i-1];
}
c[a[i]]=true;
}
System.out.println(ans);
}
else if(what == 1) { //k 번째 순열 출력
long k = scan.nextLong();
for(int i=0; i<n; i++) {
for(int j=1; j<=n; j++) {
if(c[j])
continue;
if(f[n-i-1] < k) {
k -= f[n-i-1];
}
else {
a[i] = j;
c[j] = true;
break;
}
}
}
for(int i=0; i<n; i++) {
System.out.print(a[i] + " ");
}
}
}
|
'Algorithm' 카테고리의 다른 글
| 백준 6603 로또 Java (0) | 2019.06.07 |
|---|---|
| 백준 10971 외판원 순회 2 Java (0) | 2019.05.31 |
| 백준 10974 모든 순열 Java (2) | 2019.05.28 |
| 백준 10972 이전 순열 & 10973 다음 순열 Java (0) | 2019.05.28 |
| 비트마스크 (0) | 2019.05.27 |