여러가지 방법으로 풀 수 있는 외판원 순회 2 문제를
순열을 사용한 완전 탐색으로 푸는 방법을 정리하려고 한다
문제는
n을 입력받고
n개 만큼의 도시를 전부 순서대로 이동할 때
드는 비용의 최소값을 출력하는 문제이다.
배열에 0부터 저장한다 생각하고 문제를 풀어볼 것 이다.
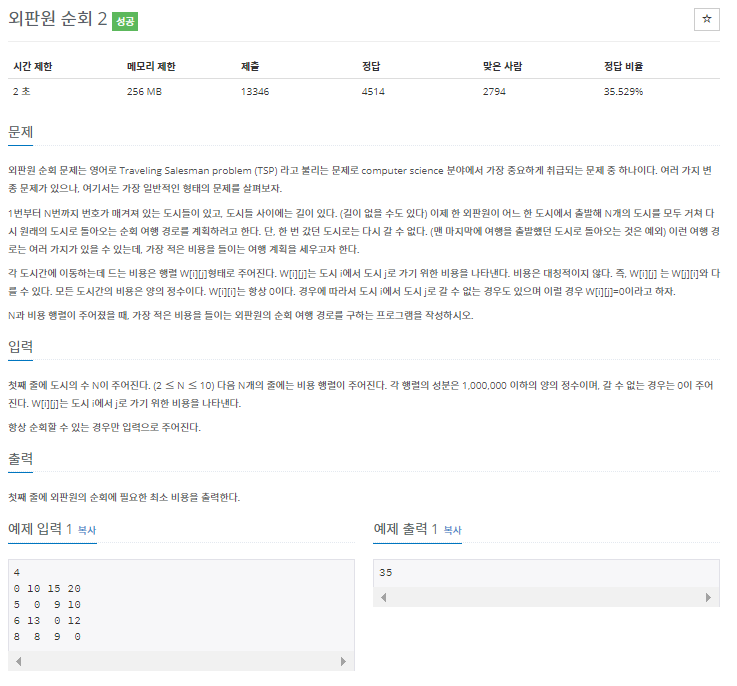
예제로 주어진
4
0 10 15 20 --> 0번
5 0 9 10 --> 1번
6 13 0 12 --> 2번
8 8 9 0 --> 3번
에서는
각각의 행에서
열은 j번째 행으로 이동할때 드는 비용을 말하는 것이다.
예를들어 0번에서 1번으로 갈땐 비용 w[0][1] -> 10이 들고
1번에서 2번으로 갈땐 비용 w[1][2] -> 9가 들고
2번에서 3번으로 갈땐 비용 w[2][3] -> 12이들고
3번에서 다시 0번으로 가는 비용은 w[3][0] -> 8이 든다.
합쳐서 총 39의 비용이 드는것이다.
이 예제의 최소값은 35로
0번에서 1번으로 10
1번에서 3번으로 10
3번에서 2번으로 9
2번에서 0번으로 6
10+10+9+6인 것이다.
나는 문제를 이해하는 것도 오래걸렸다 ㅠㅠ
N개의 도시를 각각 선택해서 가는 것이 아니라
모든 도시를 돌아야 하기 때문에
완전 탐색을 할 때
순열을 사용해서 풀어야 한다.
순열로 도시를 어떤 순서로 돌 것인지
모든 경우를 다 해보는 것이다.
N이 4일 때
{0, 1, 2, 3} , {0, 1, 3, 2} ... {3, 2, 1, 0} 처럼
순열로 N!개 만큼의 이동 순서를 구하고 그 이동 순서대로
for문을 N번 돌면서 값을 더하고 최소값을 구하면 된다.
이 문제의 N제한은 최대 10으로
도시를 돌 순열의 총 개수는 10!이고 10!은 = 3,628,800이다.
N!만큼의 순열을 N번씩 돌면서 값을 더해야 하니까
최대 10! * 10 = 36,288,000
O(N! * N)으로
1억번의 연산이 되지 않으므로 1초안에 해결할 수 있다.
하지만 생각해보면 어떻게 돌지 N!개만큼의 모든 수열을 다 돌아볼 필요는 없다.
0 -> 1 -> 2 -> 3
2 -> 3 -> 4 -> 1
3 -> 4 -> 1 -> 2
4 -> 1 -> 2 -> 3
처럼 같은 값이 나오는 수열이 많고
시작은 어차피 0번째 도시로 고정이고 원래 도시로 돌아오라는 조건 때문이다.
순열을 만드는 숫자를 0으로 고정하면
N-1 ! 개를 만드는 것이된다.
-1정도는 다른 시간복잡도에선 의미가 없지만
팩토리얼에서는 10배가 차이가 나기 때문에
결론적으론 시작 도시만 고정해도 O(N!)으로 시간복잡도를 확 줄일 수 있다.
구현은 코드를 보면서 살펴보자.
여러번 읽어보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
public class Q10971 {
static void swap(int [] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
public static boolean nextPermutation(int [] a) {
int i = a.length-1;
while(i > 0 && a[i] <= a[i-1])
i--;
if(i<=0)
return false;
int j = a.length-1;
while(a[j] <= a[i-1]) {
j--;
}
swap(a, i-1, j);
j = a.length-1;
while(i < j) {
swap(a, i, j);
i++;
j--;
}
return true;
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int [][] a = new int[n][n];
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
a[i][j] = scan.nextInt();
int [] d = new int[n-1];
//0번으로 이동하는 것을 제외한 이동값 초기화
for(int i=0; i<n-1; i++) {
d[i] = i+1;
}
int ans = Integer.MAX_VALUE;
do {
boolean ok = true;
int sum = 0;
//0번으로 이동하는 것을 제외했기 때문에 -1, 더하는 값에 i+1이 있기 때문에 -1 => n-2가 된다.
for (int i=0; i<n-2; i++) {
if (a[d[i]][d[i+1]] == 0) { //못가는 도시일 시 false
ok = false;
} else {
sum += a[d[i]][d[i+1]];
}
}
//못가는 도시가 없었고 0번째 도시에서 첫 번째 도시로 갈때 0이 아니고 마지막 도시에서 0번째 도시로 갈때 0이 아니면
if (ok && a[0][d[0]] != 0 && a[d[n-2]][0] != 0) {
sum += a[0][d[0]] + a[d[n-2]][0]; //0째번에서 첫 번째로 가는 비용 + 마지막에서 0번째로 가는 비용
if (ans > sum) {
ans = sum;
}
}
} while(nextPermutation(d));
System.out.println(ans);
}
}
|
'Algorithm' 카테고리의 다른 글
| 완전 탐색(exhaustive - search)의 종류 (0) | 2019.06.07 |
|---|---|
| 백준 6603 로또 Java (0) | 2019.06.07 |
| 백준 1722 순열의 순서 Java (0) | 2019.05.29 |
| 백준 10974 모든 순열 Java (2) | 2019.05.28 |
| 백준 10972 이전 순열 & 10973 다음 순열 Java (0) | 2019.05.28 |