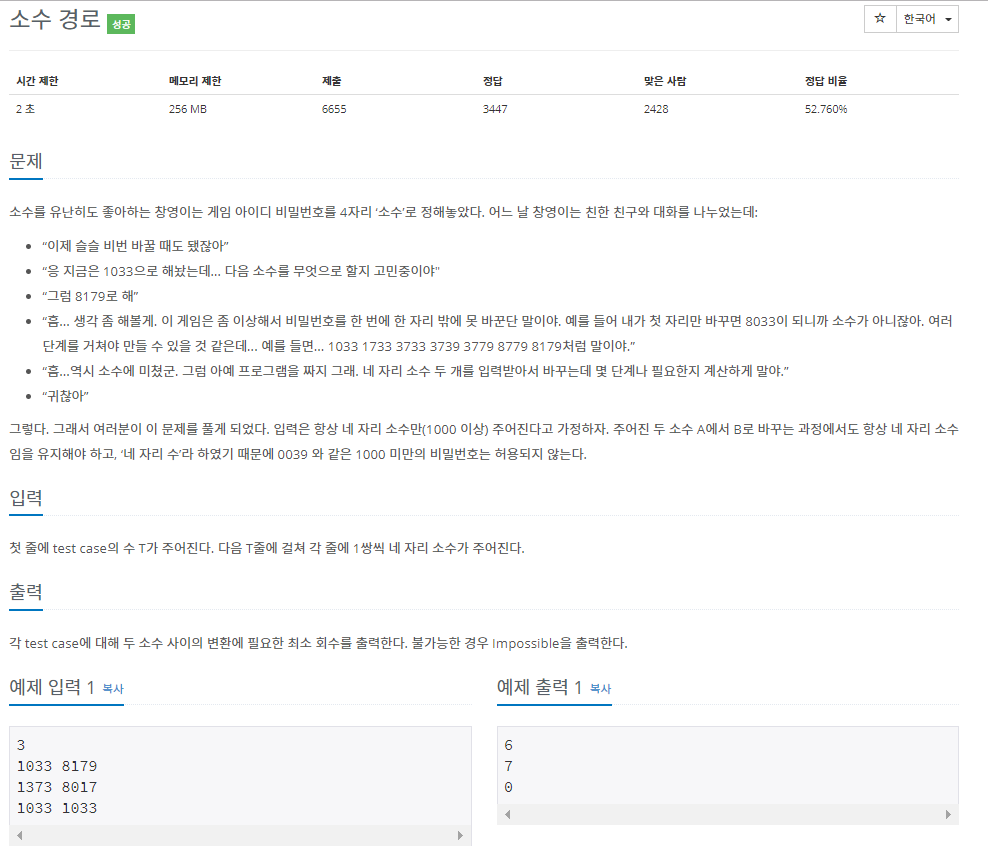
완전 탐색 문제인 소수 경로이다.
간선의 가중치가 없고
최소 회수를 구하는 문제이고
4자리의 소수들만 탐색해보면 되므로 2초는 넉넉하다.
그러므로 BFS를 사용한 완전 탐색으로 풀면 되는 문제이다.
자주 까먹는 에라토스테네스의 체를 다시 한 번 복습해 볼 수 있어서 좋은 문제였다.
소수를 한 단계씩 바꾸는 모든 경우를 어떻게 구해야하는지 헤맸는데
그냥 4자리 중에 한자리씩 0~9까지 다 바꿔보면서
그 수가 소수이면 큐에 넣어서 BFS탐색을 하면 됐었다.
수를 바꿔넣을 땐 Stringbuilder의 메소드인 setCharAt(인덱스, 바꿀 문자)를 사용했다.
StringBuilder에 유용한 메소드가 생각보다 참 많은 것 같다.
어려워보이면서도 간단한 문제이다.
다른 BFS탐색 문제랑 똑같이 구현하면 된다.
다만 바꿀 소수를 구하는 부분이 헷갈릴 수 있다.
코드를 보면서 복습해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Q1963 {
static int change(int num, int index, int v){
StringBuilder sb = new StringBuilder(String.valueOf(num));
sb.setCharAt(index, (char)(v+'0')); //int를 char로 바꾸기위해 +'0'을 해준다.
return Integer.parseInt(sb.toString());
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int tc = scan.nextInt();
//에라토스테네스의 체로 소수 구해놓기.
List<Boolean> prime = new ArrayList<>();
//0과 1을 소수가 아닌걸로 처리
prime.add(false);
prime.add(false);
for(int i=2; i<10000; i++) {
prime.add(true);
}
for(int i=2; i*i<10000; i++) {
if(prime.get(i)) {
for(int j=i*i; j<10000; j+=i) {
prime.set(j, false);
}
}
}
while(tc-- > 0) {
int n = scan.nextInt();
int m = scan.nextInt();
Queue<Integer> q = new LinkedList<>();
int [] d = new int[10000];
boolean [] b = new boolean[10000];
q.add(n);
b[n] = true;
while(!q.isEmpty()) {
int v = q.poll();
for(int i=0; i<4; i++) {
for(int j=0; j<=9; j++) {
if(i==0 && j==0) //0번째 자리를 0으로 바꾸면 안된다.
continue;
int k = change(v, i, j); //변경 가능한 수 모두 구해보기
d[k] = d[v]+1;
b[k] = true;
q.add(k);
}
}
}
}
System.out.println(d[m]);
}
}
}
|
'Algorithm' 카테고리의 다른 글
| 백준 1525 퍼즐 Java (0) | 2019.06.09 |
|---|---|
| 백준 9019 DSLR Java (0) | 2019.06.08 |
| 완전 탐색(exhaustive - search)의 종류 (0) | 2019.06.07 |
| 백준 6603 로또 Java (0) | 2019.06.07 |
| 백준 10971 외판원 순회 2 Java (0) | 2019.05.31 |